قبل از پرداختن به مقالات بعدی مواردی وجود دارد که بایستی مرور کنیم . در این پست به صورت مختصر شبکه های RNN و LSTM را مورد بررسی قرار خواهیم داد. من در این پست به صورت کلی نکات ضروی را بیان میکنم و جزییات بیشتر را به شما واگذار میکنم.

در ابتدا برداشتی که من از LSTM داشتم مثل یک جعبه جادویی بود که معلوم نبود در داخل آن چه اتفاقی رخ میدهد . اما با تحقیق بیشتر این احساس از بین رفت. اگر در ابتدای این پست احساسی شبیه شکل زیر دارید زیاد نگران نباشید چون در ادامه موارد جالبی را خواهیم آموخت و این احساس به شکلی که در انتهایی پست قرار گرفته تغییر خواهد کرد.

حضور شبکه های LSTM در سال های اخیر بسیار پر رنگ شده است . این شبکه ها در حال حاضر در تکنولوژی های پیشرفته اعم از تکنولوژی Google Voice استفاده میشو ند اما تاریخچه آن به 1995 بر میگردد.

داده های سری زمانی

بگذارید به صورت مختصر تعریف داده های سری زمانی را قبل از ورود به قسمت اصلی را توضیح دهیم . همانطور که از نام آن پیداست داده های سری زمانی به مجموعه داده هایی گفته میشود که در فواصل زمانی منظمی جمع آوری شده اند :

x_1, x_2, x_3, ..., x_T

این داده ها میتوانند دنباله ای از فریم های یک انیمیشن،کلمات یا حروف یک جمله، امواج صوتی (که با یک بازه زمانی مساوی نمونه گیری شده اند) و … باشند . نمونه ای از مسایل دادا های سری زمانی به شکل زیر هستند:

👌تولید جملات و دیابوگ

👌باز تشخیص صدا /آواها

👌بازتشخصی ویدئو و …

اما LSTM چگونه این مسائل را حل میکند؟ به صورت مختصر در مسئله تولید جملات LSTM میتواند کلمه بعدی را با توجه به کلماتی که از طریق ورودی به آن داده شده است پیش بینی کند. در فرآیند آموزش ، این شبکه قوانین گرامر را فرا میگیرید .

RNN(شبکه عصبی بازگشتی) چیست ؟

این شبکه ها در واقع برای پردازش سیگنال های دنباله دار به وجود آمدند. در یک شبکه عصبی معمولی تمام ورودی ها و خروجی ها مستقل از یکدیگر هستند،اما در بسیاری از موارد این ایده میتواند خیلی بد باشد. به عنوان مثال فرض کنید شما در یک جمله به دنبال پیش بینی کلمه بعدی هستید در صورتی که شبکه نتواند روابط بین کلمات را یاد بگیرد مسلما نمی تواند کلمه بعدی را به درستی پیش بینی کند.

بگذارید با یک دیدگاه دیگر به این نوع شبکه نگاه کنیم، این شبکه ها دارای یک نوع حافظه هستند که اطلاعاتی تا کنون دیده است را ضبط میکند. در تئوری اینطور به نظر میرسد که این شبکه ها میتوانند اطلاعات موجود در یک دنباله طولانی را ضبط و از آنها استفاده کنند اما در عمل اینطور نیست و بسیار محدود هستند، به این صورت که فقط اطلاعات چند گام قبل را ضبط میکنند. در شکل زیر نمونه ای از یک RNN معمولی نمایش داده شده است.

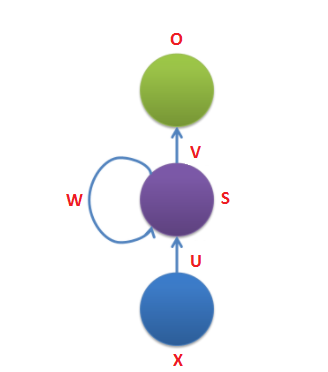
در شکل بالا X ورودی در گام زمانی t است، این ورودی میتواند یک بردار one-hot باشد (one-hot برداری است در یک بعد ۱ و در بقیه ابعاد صفر است(.

S حالت پنهان در گام زمانی t است. این قسمت همان جایی است که حافظه شبکه در آن قرار گرفته است. S بر اساس حالت پنهان قبلی و ورودی که در زمان جاری به آن داده میشود تغییر میکند.که به شکل s(t)=f(Ux(t)+W(s(t-1)) است.تابع f معمولا یک تابع غیر خطی مثل tanh یا ReLU است.

O خروجی در گام زمانی t است.به عنوان مثال در محاسبه کلمه بعدی در یک جمله این خروجی میتواند یک بردار از احتمالات در واژگان ما باشد.

چند نکته وجود دارد که بایستی آنها را بدانیم :

همانگونه که در بالا توضیح داده شد حالت پنهان شبکه S در واقع جایی است که حافظه شبکه در آن قرار گرفته است . S اطلاعاتی در باره اینکه تا کنون در شبکه چه رخ داده است را ضبط میکند. خروجی S با توجه به حالات قبلی محاسبه میشود اما همانطور که بیان شد S نمیتواند اطلاعات موجود در گام های زمانی (به عنوان مثال 10 گام قبل) را ضبط کند.

برخلاف شبکه های معمولی که از پارامتر های متفاوتی در هر لایه استفاده میکند، یک شبکه RNN پارامتر های مشابهی را بین همه گام های زمانی به اشتراک میگذارد .(U,V,W) این بدین معنی است که ما در هر گام زمانی عملیات مشابهی را انجام میدهیم فقط ورودی ها متفاوت هستند. با این تکنیک تعداد کلی پارامتر ها یی که شبکه بایستی یاد بگیرد به شدت کاهش پیدا میکند.

اصلی ترین ویژگی RNN حالت پنهان آن است که اطلاعاتی یک توالی را ذخیره میکند. همچنین حتما نیاز نیست ما در هر گام زمانی یک خروجی و یا حتما یک ورودی داشته باشیم. بر اساس کار مورد نظر این دیاگرام میتواند تغییر کند.

شبکه های RNNs به این علت بازگشتی نامیده میشوند که خروجی هر لایه به محاسبات لایه های ماقبل آن وابسته است. به عبارتی دیگر این شبکه ها دارای حافظه هستند که اطلاعات مربوط به داده های دیده شده را ذخیره میکند. در نگاه اول شاید کمی عجیب به نظر برسد اما این شبکه ها در واقع کپی های متعدی از شبکه های عصبی معمولی هستند که کنار هم چیده شده اند و هر کدام پیغامی را به دیگری انتقال میدهند.

LSTM چیست؟

LSTM (به معنی حافظه طولانی کوتاه-مدت) مخفف کلمه Long short-term memory یک نوع مدل یا ساختار برای داده های ترتیبی است که در سال 1995 برای توسعه شبکه های عصبی بازگشتی(RNN) ظهور پیدا کرد. Sepp Hochreiter در مقاله LSTM توضیح میدهد که عبارت long term memory به وزن های یادگرفته شده و short term memory به حالت های درونی سلول ها اطلاق میشود. LSTM برای حل مشکل پدیده ناپدید شده گرادیان در شبکه های عصبی بازگشتی بوجود آمدند که تغییر عمده آن جایگزین کردن لایه میانی RNN با یک بلاک که بلاک LSTM نام دارد است.

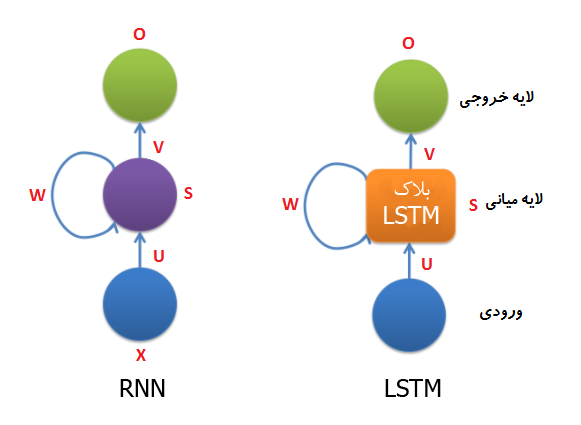
بزرگترین ویژگی LSTM امکان یادگیری وابستگی بلند مدت است که توسط شبکه های عصبی بازگشتی امکان پذیر نبود. برای پیش بینی گام زمانی بعدی نیاز است که مقادیر وزن ها در شبکه بروز رسانی شوند که این کار مستلزم حفظ اطلاعات گام های زمانی ابتدایی است. یک شبکه عصبی بازگشتی فقط میتواند تعداد محدودی از وابستگی های کوتاه مدت را یاد بگیرد ، اما سری های زمانی بلند مدت مثل 1000 گام زمانی قایل یادگیری توسط RNN ها نیستند اما LSTM ها میتواند این وابستگی های بلند مدت را به درستی یاد بگیرند. همانگونه در جدول ذیر (این جدول از مقاله Sepp Hochreiter استخراج شده است ، اطلاعات بیشتر ) نمایش داده شده است RNN نتوانست حتی خروجی شبکه با delay 100 را با هر دو متد RTRL, BPTT پیش بینی کند اما LSTM در زمان کوتاه توانست این کار را انجام دهد..

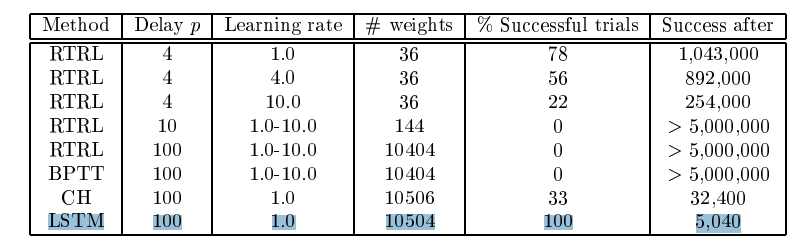
قبل از ورود به جزییات ساختار LSTM، ابتدا نیاز است پدیده ناپدید شدن گرادیان که اولین بار در سال 1991 توسط Hochreiter در پایان نامه ایشان شرح داده شد را بررسی کنیم. دو متد برای آموزش شبکه های RNN وجود دارد:

Back-Propagation Through Time) یا BPTT

Real-Time Recurrent Learning یا RTRL

هر دوی این الگوریتم ها بر پایه مشتق گیری کار میکنند.گرادیان الگوریتم هایی از این نوع در انتشار رو به عقب در سری هایی با وابستگی بلند مدت، ممکن است نا پدید یا به بینهایت میل کنند. این مشکل نه تنها در RNN ها بلکه در شبکه های عمیق عصبی جایی که گرادیان از میان چندین گام عبور میکند نیز رایج بود. مکانیسمی که باعث میشود شبکه های عصبی یاد بگیرند بطور غیر قابل باوری ساده است ، این مکانیسم stochastic gradient descent نام دارد. به صورت خلاصه برای هر پارامتر در شبکه ما (وزن ها و بایاس ها)،کاری که ما بایستی انجام دهیم محاسبه مشتق تابع هزینه نسبت به پارامتر ها و حرکت دادن آن به مقدار کم در سمت مسیر مخالف آن است.

این الگوریتم بسیار ساده، در برخی از شبکه ها رفتار عجیب و غریبی نشان میدهد، بطوری که وزن هایی که نزدیک تر به انتهای شبکه هستند نسبت به وزن های موجود در لایه های اولیه با مقدار خیلی بیشتری تغییر میکنند.هر چه تعداد لایه های شبکه ما بیشتر باشد مقدار پارامتر های لایه های اول، کمتر تغییر میکند و این مشکل ساز است زیرا مقادیر وزن ها در ابتدای کار به صورت تصادفی مقدار دهی میشوند و اگر این مقادیر به ندرت تغییر کنند، یا هیچ وقت نمیتوانند مقدار صحیح را پیدا کنند یا این فرآیند خیلی خیلی زمانبر خواهد بود.

برای شفافتر شدن این موضوع یک شبکه ساده برای طبقه بندی عکس های موجود در دیتابیس MNIST آموزش داده شد. در شکل زیر تغییرات گرادیان در طول زمان در لایه های مختلف شبکه نمایش داده شده است:

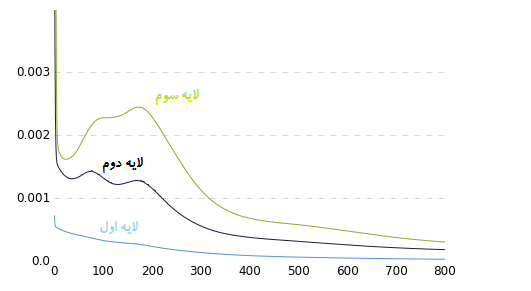
توجه کنید که چقدر مقدار گرادیان در لایه اول نسبت به لایه سوم کمتر است، این نمودار نمایش میدهد که مقادیر وزن ها به مقدار به مراتب خیلی کمتری از لایه های دیگر تغییر میکنند.این فقط برای یک شبکه خیلی کوچک است موضوع خیلی جدی تر خواهد شد اگر ما تعداد این لایه ها را افزایش دهیم. از آنجایی که بقیه شبکه با مقادیر پارامتر های موجود در لایه های اولیه تحت تاثیر قرار میگیرند، اگر این پارامتر ها کاملا ناصحیح باشند شبکه ما به صورت صحیح عمل نخواهد کرد.

چرا گرادیان نا پدید میشود؟

با یک مثال ساده این موضوع را به صورت قدم به قدم پیش میبریم.فرض کنید که یک شبکه با سه لایه داریم. برای سادگی فرض میکنیم هر کدام از لایه ها فقط یک نرون دارند:

هر نرون با یک w (وزن) در ارتباط است و خروجی آن تابعی از w در مقدار ورودی است.به عنوان مثال نرون اول خروجی W1xX را تولید میکند . در عمل این تابع میتواند sigmoid،tanh یا تابع ReLU باشد، اما در اینجا ما این تابع را f(x) مینامیم. از اینجا به بعد خروجی این تابع برای نرون n را z(n) مینامیم:

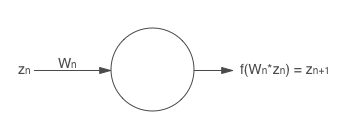
در انتها،شبکه ما با تابع هزینه به پایان میرسد که این تابع تفاوت این مقدار حقیقی و مقدار تولید شده را محاسبه میکند که میتواند تابعی مثل cross-entropy باشد. این تابع در واقع خروجی لایه انتهایی خواهد شد. اکنون بیاید الگوریتم انتشار رو به عقب را بررسی کنیم . در اولین گام بایستی مقدار W3 را بروز رسانی کنیم.

بدین منظور، نیاز است که مشتق تابع هزینه نسبت به W3 محاسبه شود. اگر ما قاعده زنجیری را در این رابطه اعمال کنیم:

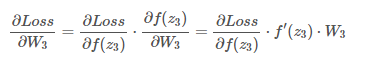
مقدار W3 را اندکی در مسیر مخالف حرکت میدهیم.برای لایه های قبلی این عملیات مجدد تکرار میشود. بیاید پرش کنیم به ابتدای شبکه و ببینیم چگونه وزن اولین لایه تغییر میکند:

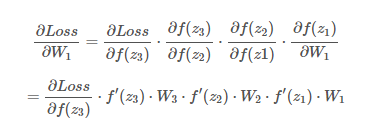
توجه کنید که برای محاسبه گرادیان برای W1 تعداد عبارت ها افزایش پیدا میکند. متد رایج برای مقدار دهی اولیه پارامتر ها در یک شبکه عصبی به فرم یک تابع گوسی با میانگین صفر و انحراف معیار یک است، که این گویای این موضوع است که اندازه پارامتر های شبکه (وزن ها) کمتر از یک است. اگر تابع f(x) ما یک تابع sigmoid باشد آنگا مشتق همیشه کمتر از 0.25 خواهدشد.حالا در نظر بگیرید اگر تعداد زیادی از این اعداد کوچک در یکدیگر ضرب شوند باعث ایجاد یک عدد خیلی خیلی کوچک خواهند شد. سناریوی مخالف این شرایط نیز میتواند اتفاق بیفتد به طوری که مقدار وزن ها بزرگ شوند آنگا ضرب این اعداد در یک دیگر باعث مشود گرادیان به بی نهایت میل کند.

شبکه های lstm در نگاه اول پیچیده به نظر می‌رسند ، به همین دلیل در ادامه بحث قصد داریم این ساختار را به چند قسمت تقسیم کنیم و یکی یکی آنها را بررسی کنیم .بدین منظور نیاز است که به چند سال قبل بازگردیم و چند تا مقاله جالب را با هم مرور کنیم . این مقاله ها عبارتند از :

(1) Original (95, 97) Hochreiter & Schmidhuber, 95; 97

(2) Introduction of Forget Gate (1999) Gers & Schmidhuber, 99

(3) Introduction of Peephole Connection (2000)Gers & Schmidhuber, 2000

اولین نسل lstm ( سال ۱۹۹۵ و ۱۹۹۷)

ساختار اولین بلاک lstm در شکل زیر نمایش داده شده است :

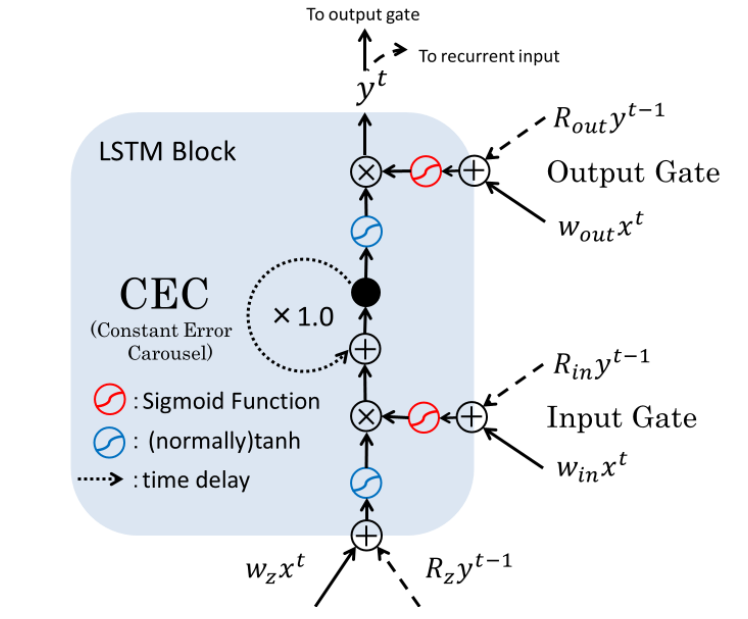
قبل از توضیح شکل بالا ابتدا بیاید با هم انتشار خطا از یک واحد u به v را آنالیز کنیم. شرایطی را در نظر بگیرید که خطای محاسبه شده توسط u در گام زمانی t به اندازه q واحد زمانی به سمت واحد v به سمت عقب انتشار داده میشود. این عملیات باعث میشود خطای تولید شده به اندازه فاکتور زیر افزایش یابد:

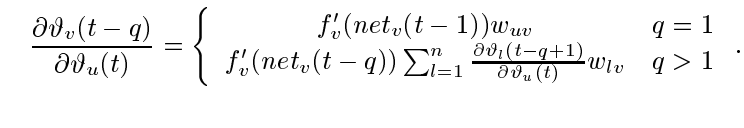
مجموع این عبارت از مسیر lq=v به l0=u :

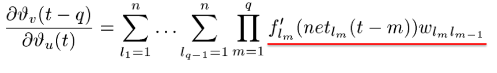
در صورتی که مقدار عبارت (که با رنگ قرمز مشخص کردم) همیشه از 1 بیشتر شود گرادیان ناپدید میشود و در صورتی که این مقدار همیشه کمتر از یک باشد گرادیان ناپدید میشود.

در تابع سیگمید مقدار مشتق عبارت f(…) حداکثر 0.25 است و در این شرایط گرادیان ناپدید خواهد شد.

توجه کنید که در شکل بالا و شکل هایی که در ادامه قرار داده خواهد شد فلش هایی که به صورت نقطه چین هستند به حافظه قبل یا ورودی های بلاک قبلی اشاره دارند.

اما این مشکل را چگونه میشود حل کرد؟

برای حل این مشکل نیاز به یک تابع فعال ساز داریم که که مقدار ثابتی در طول زمان داشته باشد.

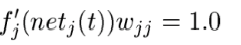
بدین منظور همانگونه که در شکل بالا نشان داده شده است ما از یک تابع همانی با وزن 1 استفاده میکنیم که CEC )مخفف عبارت Constant Error (Carrousel نام دارد.( به عبارت ساده CEC یک نرون است که دارای یک اتصال به خودش با وزن یک است) با استفاده از این متد سیگنال خطا میتواند در زمان انتشار رو به عقب بدون از دست دادن اعتبارش در مسیر جریان داشته باشد.بگذارید سه خصوصیت یک واحد CEC را در یک لیست قرار بدیم چون خیلی مهم (و همچنین ساده) هستند:

👌یک اتصاص برگشتی

👌یک تابع فعال سازf

👌تابع همانی

اما دلیل استفاده از دو گیت ورودی و خروجی چیست؟

جواب کوتاه: برای حل دو مشکل عمده CEC ، تداخل سیگنال ورودی و خروجی!

جواب بلند: بگذارید با یک مثال ساده ضرورت این گیت ها را نمایش دهیم. مشکل دیاگرام ساده (بدون گیت) این است که این ساختار باعث به وجود آمد ناثباتی در شبکه میشود. در شکل زیر یک اتصال از نود ورودی l به نود پنهان j (با یک اتصال برگشتی) و سپس نود خروجی k وجود دارد.

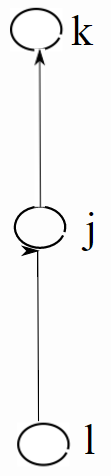
در این ساختار وزن ورودی دچار تداخل میشود. در فرآیند آموزش پارامتر های l و j در فعال سازی یا عدم فعال سازی نرون j دخالت دارند به طوریکه برخی از آنها برای ذخیره کردن سیگنال در نرون j و بر خی از آنها برای محافظت از آن تلاش میکنند. اگر ما هیچ گیتی برای کنترل این جریان نداشته باشیم وزن ها دچار تداخل میشوند که این تداخل فرآیند آموزش را سخت میکند. برای رفع این مشکل از گیت ورودی استفاده میشود. برای گیت خروجی نیز مشکل مشابهی وجود دارد که این مشکل از طریق قرار دادن یک گیت خروجی برطرف میشود. در واقع این دو گیت مثل چند شیر تنظیم کننده کار میکنند. شکل زیر را در ذهن داشته باشد.

نسل دوم LSTM معرفی گیت فراموشی

هر چند LSTM در همان سالها موفقیت های قابل توجهی در کارهای مربوط به داده های سری زمانی بدست آورده بودند اما یک ضعف عمده داشت. شبکه به صورت مداوم داده های را از واحد های ورودی دریافت میکند و این اطلاعات به صورت پیوسته در سلول حافظه نوشته میشوند. اگر سلول یاد نگیرد که مقدار خودش را ریست (فراموش) کند این مقدار ممکن است به صورت نا محدود رشد کند که باعث میشود شبکه از کار بیفتد.متد پیشنهاد گیت فراموشی بود که این توانایی به یک سلول LSTM میدهد که چه هنگام مقدار خودش را در زمان مناسب ریستارت کند . این گیت مستقیما به بدنه سلول متصل است.

برای طولانی نشدن این پست موارد کلیدی این مقاله به صورت خلاصه بیان شد.پیشنهاد میکنم بخش 2.1 (محدودیت های LSTM ) و بخش 6 (شبه کد) مقاله را برای جزییات بیشتر مطالعه کنید.

نسل سوم : معرفی اتصال peephole

هر چند ساختار LSTM کامل به نظر میرسد اما همانطور که در شکل قبلی پیدا است سلول حافظه در کنترل سایر گیت ها نقش خاصی را ندارد. در این مقاله اتصال هایی با نام peephole معرفی شدند . با این اتصال گیت ورودی و فراموشی یک ورودی از سلول موجود در گام زمانی قبلی دریافت میکند و گیت خروجی یک ورودی از سلول موجود در گام زمانی کنونی دریافت میکند

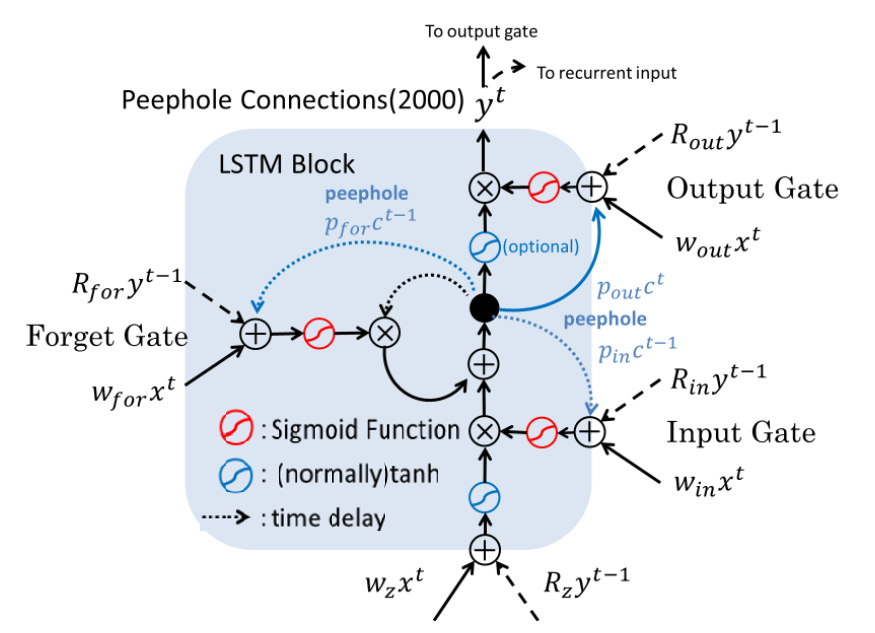
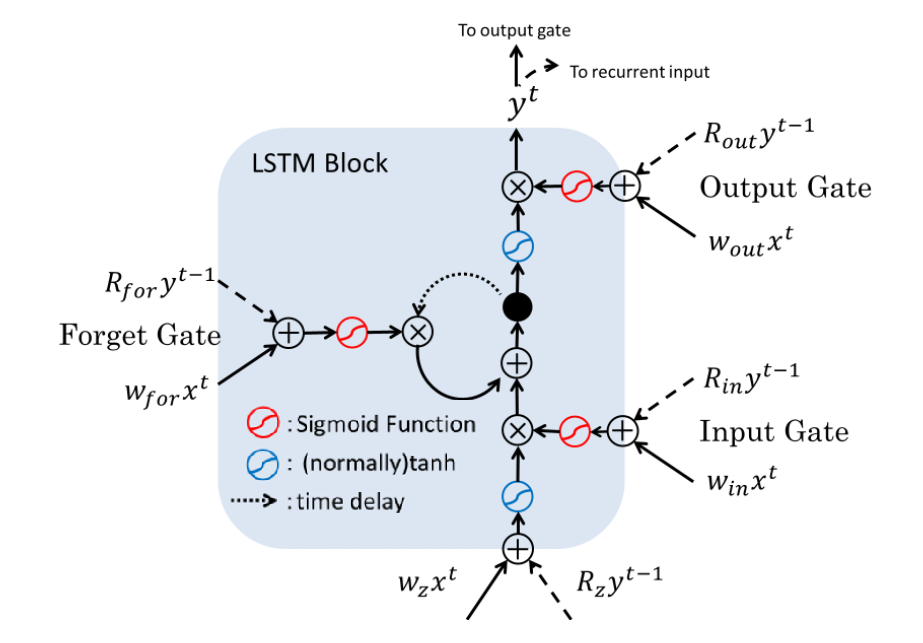
در بالا خلاصه ای از مقاله های مختلف که تکمیل کننده بلاک LSTM امروزی هستند را بررسی کردیم.حالا نوبت به این رسیده که بررسی کنیم این اجزا چگونه در کنار یکدیگر کار میکنند. بدین منظور از دیاگرام زیر که دیاگرام یک بلاک LSTM است برای توضیحات تکمیلی استفاده میکنیم .( این دیاگرام برگفته شده از فایل پاورپوینت Shi Yan است که در repository گیت هاب ایشان قرار گرفته است برای دانلود بر روی این لینک کلیک کنید)

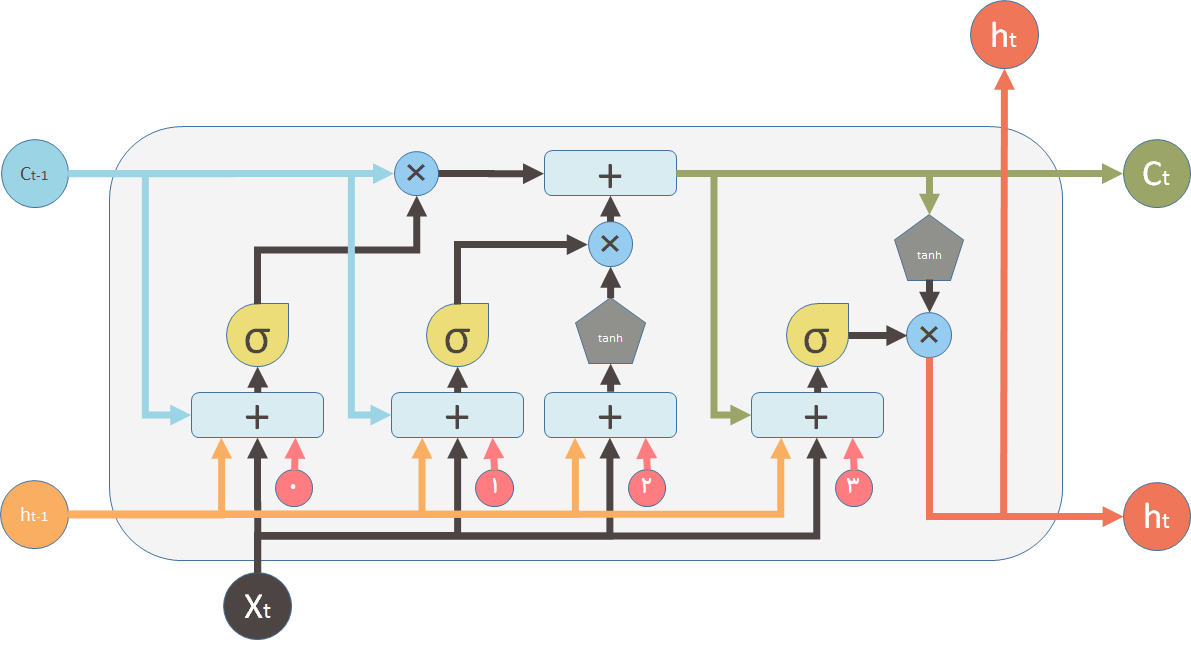
هر کدام از اشکال استفاده شده در دیاگرام بالا در این شکل توضیح داده شده اند:

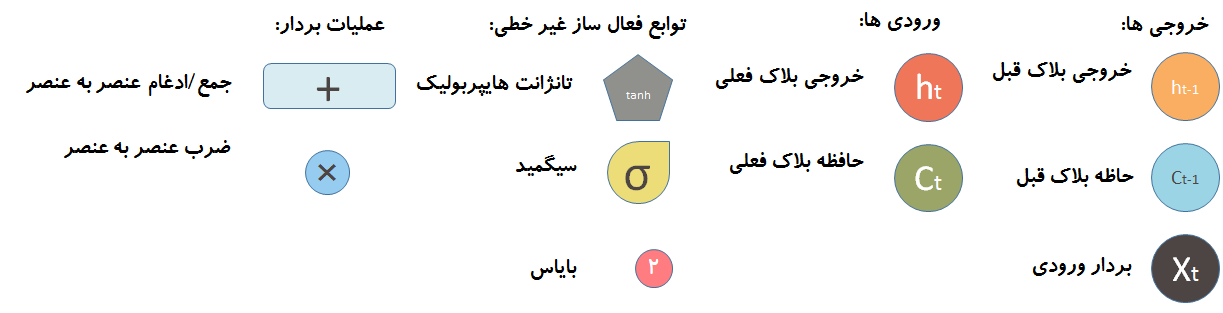دیاگرام بالا کمی پیچیده به نظر میرسد. برای سادگی بیایید اجزای داخلی را در نظر نگیریم. شبکه سه ورودی را دریافت میکند.

X_t ورودی گام کنونی

h_t-1 خروجی بلاک LSTM قبلی

C_t-1 خروجی سلول حافظه بلاک LSTM قبلی

خروجی ها:

Ht خروجی گام زمانی t

C_t حافظه سلول کنونی

در نتیجه هر واحد بر اساس ورودی کنونی، خروجی واحد پیشین و حافظه واحد قبل تصمیم گیری میکند سپس یک خروجی جدید را ایجاد و مقدار حافظه اش را اصلاح میکند.

C_t(حافظه سلول) توسط دو مقدار تغییر میکند . مقدار اول گیت فراموشی است . اگر این گیت کاملا بسته شود، حفظه کاملا پاک میشود اما اگر باز باشد تمام مقدار حافظه قبلی از آن عبور میکند. دوم مقدار حافظه جدید است. حافظه جدید با حافظه قبلی ادغام میشود. اینکه چه مقدار حافظه جدید بایستی وارد شود توسط مقدار دوم کنترل میشود.

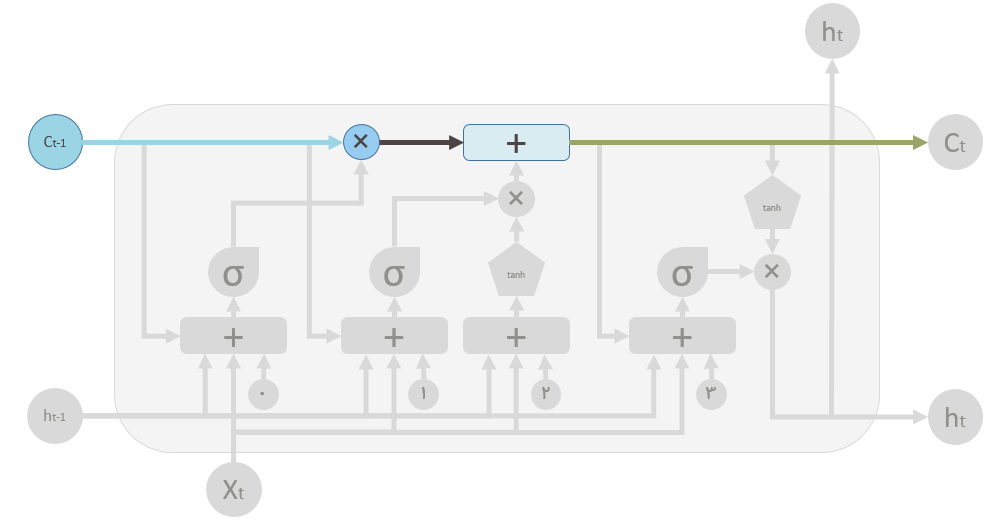
در دیاگرام LSTM فلش بالا (رنگی) مسیر حافظه است که ورودی آن مقدار حافظه قبلی است. علامت ✖ همانطور که در بالا نشان داده شده است یک عملیات ضرب عنصر به عنصر است. مقدار حافظه قبلی در مسیر ورودش از گیت فراموشی عبور میکند . نتیجه این عملیات مشخص میکند که آیا مقدار حافظه قبلی نگه داشته شود یا خیر . بطور مثال اگر نتیجه ضرب C_t با این خروجی این گیت نزدیک صفر باشد به این معنی است که شما میخواهید بیشتر حافظه قبلی را فراموش کنید اما در صورتی که 1 باشد بدین معنی است که شما می خواهید مقدار مقدار حافظه قبلی به صورت کامل عبور کند. در مرحله دوم نتیجه عملیات از از عملگر + (جمع عنصر به عنصر) عبور میکند. این عملگر وظیفه ادغام حافظه قبلی و حافظه کنونی را بر عهده دارد. اینکه چقدر از حافظه جدید بایستی به حافظه قبلی اضافه شود توسط عملگر ✖ که در زیر عملگر + قرار گرفته است مشخص میشود.بعد اجرای این عملیات حافظه قبلی ( C_t-1) به حافظه جدید C_t تغییر میکند.

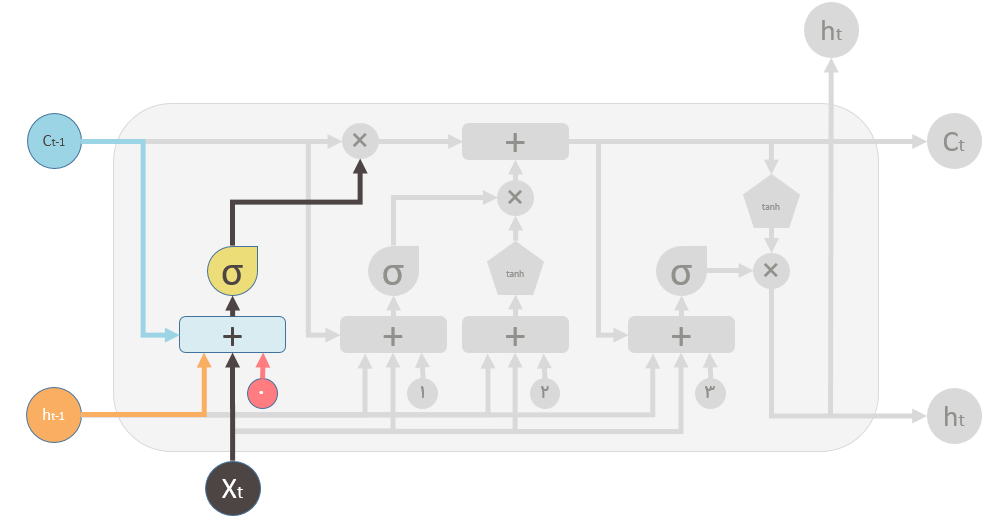
در شکل بالا گیت فراموشی مشخص شده است این گیت در واقع یک شبکه عصبی کوچک است که سه ورودی و یک بایاس را دریافت میکند و از یک تابع سیگمید به عنوان تابع فعال ساز استفاده میکند.خروجی این شبکه مقدار فراموشی است.

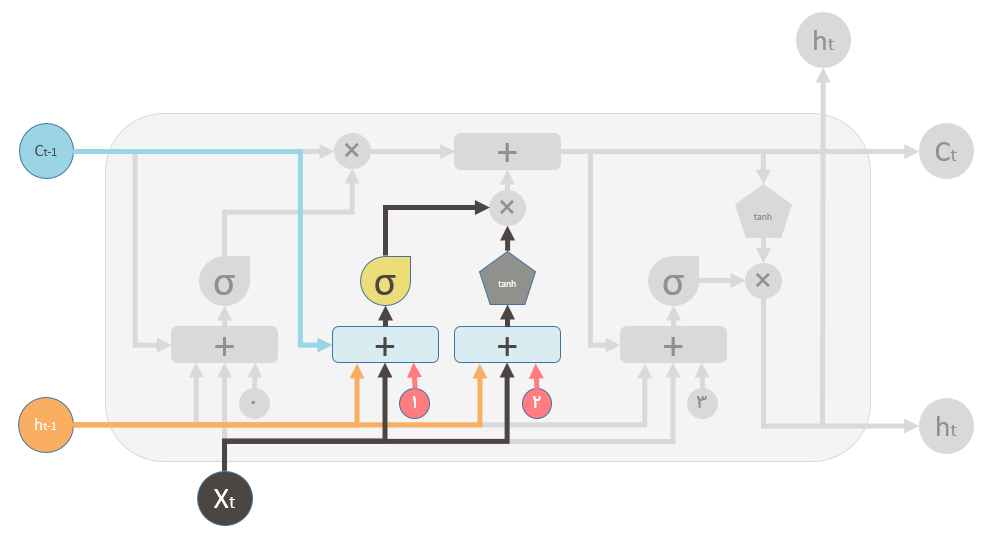
در شکل بالا نیز یک شبکه عصبی یک لایه کوچک مشخص شده است که ورودی هایی مشابه با گیت فراموشی دریافت میکند. خروجی این شبکه مشخص میکند که حافظه جدید چقدر بایستی بر روی حافظه قبلی تاثیر بگذارد. هر چند خود حافظه جدید توسط یک شبکه دیگر تولید میشود که یک شبکه یک لایه است، اما از تابع tanh به عنوان تابع فعال ساز استفاده میکند.

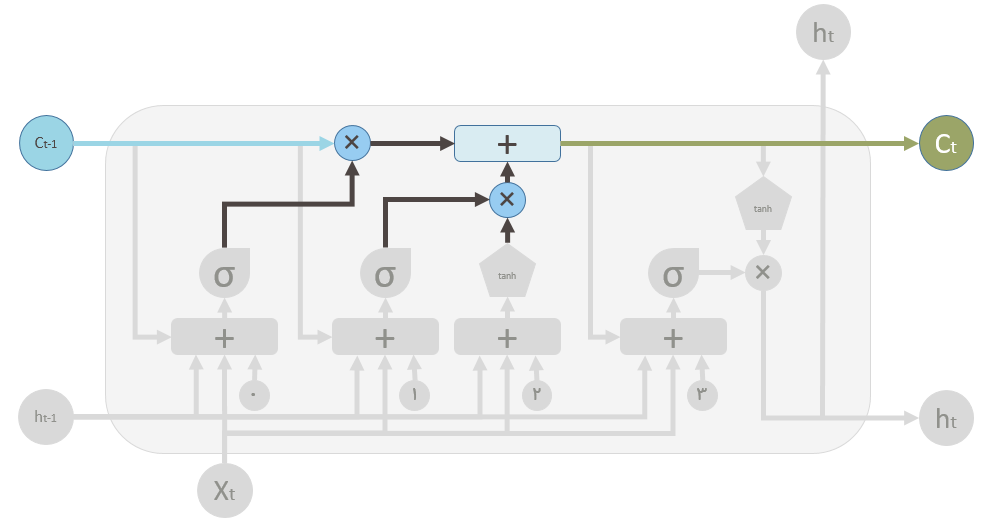
دو علامت ✖ مقادیر گیت فراموشی و مقدار حافظه جدید هستند.

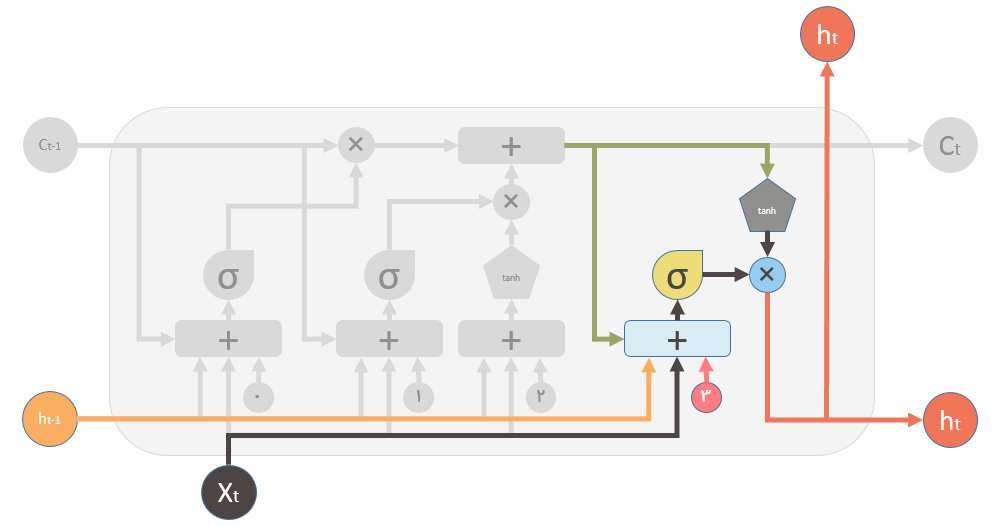
در پایان نیاز است که خروجی بلاک LSTM تولید شود. آخرین گام دارای یک خروجی است که توسط حافظه جدید و سایر اجزا مشخص شده در شکل کنترل میشود. این پست در اینجا به پایان میرسد اما موارد دیگری وجود دارد که توضیحشان خارج از حوصله این پست است به عنوان مثال مواردی مثل Gradient Clipping، Gated Recurrent Unit, attention mechanism, backpropagation through time که در پست های بعدی بنا به ضرورت بحث و بررسی خواهند شد.

مسیر نسبتا طولانی را با هم طی کردیم، امیدوارم همانطور که در ابتدای پست گفتم احساس زیر بهتون دست داده باشد🙂